Home » Telugu » జామెట్రీ » క్రమరహిత చతుర్భుజ విస్తీర్ణ కాలిక్యులేటర్
4-ముఖముల క్రమరహిత చతుర్భుజ వైశాల్యాన్ని లెక్కించుట
క్రమరహిత చతుర్భుజం(irregular quadrilateral) యొక్క వైశాల్యాన్ని 4 భుజాలు మరియు ఏదైనా కోణం(angle) లేదా వికర్ణాన్ని(diagonal) తెలుసుకోవడం ద్వారా లెక్కించవచ్చు. ఈ కాలిక్యులేటర్ విద్యార్థులు, ఇంజనీర్లు మరియు ఏదైనా నిజ జీవితంలోని నాలుగు వైపుల వస్తువు యొక్క వైశాల్యాన్ని లెక్కించడంలో ఆసక్తి ఉన్న ఎవరికైనా ఉపయోగపడుతుంది. మనం దీనిని క్రమరహిత దీర్ఘచతురస్ర ప్రాంత కాలిక్యులేటర్గా కూడా ఉపయోగించవచ్చు.
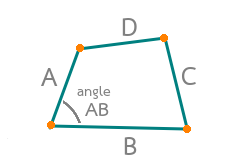
4 భుజాలు మరియు ఒక కోణాన్ని (360 డిగ్రీ విధానము) నమోదు చేయండి
చతుర్భుజం అనేది 4-వైపుల బహుభుజి. క్రమరహిత చతుర్భుజం అనేది చతురస్రం, దీర్ఘచతురస్రం, సమాంతర చతుర్భుజం, రాంబస్ మొదలైన ఏ ప్రసిద్ధ రూపానికి సరిపోని చతుర్భుజం. క్రమరహిత బహుభుజికి అన్ని భుజాలు ఉంటాయి మరియు అన్ని కోణాలు సమానంగా ఉంటాయి. క్రమరహిత చతుర్భుజం ఒక సాధారణ బహుభుజి కాదు.
కుంభాకార చతుర్భుజం: చతుర్భుజంలోని అన్ని అంతర్గత కోణాలు 180 డిగ్రీల కంటే తక్కువగా ఉంటాయి.
పుటాకార చతుర్భుజం: అంతర్గత కోణాలలో ఒకటి 180 డిగ్రీల కంటే ఎక్కువగా ఉంటుంది.
వృత్తం జ్యా మరియు పరిమితులను లెక్కించడానికి ఇతర జ్యామితి కాలిక్యులేటర్లను చూడండి.
క్రమరహిత చతుర్భుజ ప్రాంత కాలిక్యులేటర్ను ఎలా ఉపయోగించాలి
- క్రమరహిత చతుర్భుజం యొక్క అన్ని భుజాలు మరియు ఒక కోణ విలువలను తెలుసుకోండి. లేదా అన్ని భుజాలు మరియు చతుర్భుజం యొక్క ఏదైనా ఒక కోణాన్ని కొలవండి.
- A తో ప్రారంభమై D తో ముగిసే విధంగా క్రమంగా భుజాలను వరుసగా పేర్కొనండి. ఆసన్న భుజాల పేర్లతో, భుజముల మధ్య గల కోణములకు పేర్లు ఇవ్వండి.
- ఉదాహరణకు, B మరియు C భుజాల మధ్య కోణాన్ని BC అని పిలుస్తారు, AB మరియు CD మూలల మధ్య వికర్ణాన్ని(diagonal) AB-CD అని పిలుస్తారు.
- A,B,C,D అనే పేర్ల ప్రకారం కాలిక్యులేటర్లో భుజాల విలువలను నమోదు చేయండి.
- క్లిక్ చేయగా కిందకు వచ్చే మెను(drop-down menu) నుండి కోణం లేదా వికర్ణం పేరును ఎంచుకోండి. టెక్స్ట్ ఫీల్డ్ క్రింద సంబంధిత విలువను నమోదు చేయండి.
- లెక్కించు బటన్ను క్లిక్ చేయడం ద్వారా ఫలితంగా వచ్చే క్రమరహిత చతుర్భుజం లేదా క్రమరహిత దీర్ఘచతురస్రం వైశాల్యం తక్షణమే చూపబడుతుంది.
క్రమరహిత చతుర్భుజం యొక్క వైశాల్య ప్రాంతం సమస్యకు పరిష్కార విధానము
క్రమరహిత చతుర్భుజ వైశాల్యాన్ని సొంతంగా లెక్కించడానికి ఇది ఒక సంక్షిప్త విధాన పద్ధతి. క్రమరహిత చతుర్భుజం యొక్క వివిధ పరిమితులకు, వైశాల్యాన్ని ఎలా లెక్కించాలో క్రింద వివరించబడింది.
నాలుగు వైపులా మరియు ఒక వికర్ణం
చతుర్భుజాన్ని రెండు త్రిభుజాలుగా విభజించవచ్చు. రెండు త్రిభుజ ప్రాంతాల మొత్తమే కావాల్సిన వైశాల్యం.
నాలుగు భుజాలు మరియు ఒక కోణం
ఇచ్చిన కోణం లంబ కోణం అయితే, పైథాగరస్ సిద్ధాంతం ఉపయోగించి వికర్ణ దూరం లెక్కించబడుతుంది. ఇక్కడ మనకు రెండు త్రిభుజాలు ఉన్నాయి మరియు అది మొదటి సందర్భంలో వలె పరిష్కరించబడుతుంది.
ఇచ్చిన కోణం 90 డిగ్రీల కంటే తక్కువ లేదా ఎక్కువ ఉంటే.
- తెలిసిన కోణం ఏ వైపుకు జతచేయబడిందో ఆ భుజంను ఆధారం గా పరిగణించి, తెలిసిన కోణానికి ఎదురుగా వికర్ణాన్ని గీస్తే అది త్రిభుజాన్ని ఏర్పరుస్తుంది.
- మూలాధార ముగింపు బిందువులను మొదటి మరియు రెండవవిగా, త్రిభుజం యొక్క మరొక ముగింపు బిందువును మూడవవిగా సూచించండి. మూడవ ముగింపు బిందువు నుండి మూలాధారానికి లంబ రేఖను గీసి, దానికి నిలువు రేఖ అని పేరు పెట్టండి.
- త్రిభుజం యొక్క ఒక కోణం మరియు ఒక వైపు(ఆధార భుజం) మనకు తెలిసినందున త్రికోణమితిని ఉపయోగించి నిలువు రేఖను పరిష్కరించండి.
- త్రికోణమితి సూత్రాలను ఉపయోగించి నిలువు రేఖ మరియు చతుర్భుజ వికర్ణంతో ఏర్పడిన లంబ కోణ త్రిభుజం యొక్క ఆధారాన్ని కూడా పరిష్కరించండి.
- ఇప్పుడు లంబకోణ త్రిభుజం యొక్క కర్ణం అంటే వికర్ణం. ఒకసారి వికర్ణాన్ని లెక్కించిన తర్వాత, వికర్ణంతో క్రమరహిత చతుర్భుజం యొక్క వైశాల్యాన్ని లెక్కించే మొదటి పరిక్రియను అనుసరించితే వైశాల్యము పరిష్కరించబడుతుంది.